Lorenzo Díaz Cruz
En física suele ocurrir que al descubrir cierto fenómeno, aparece primero como un conocimiento muy especializado, propio de una sub-disciplina de la física, pero luego, cuando dicho fenómeno se estudia más a fondo, se descubren características más universales, que lo hacen aún más interesante. En algunos casos es posible construir un modelo matemático que permite describir las características esenciales del fenómeno de forma cuantitativa, cuyas soluciones muestran una regularidad que aclaran sus implicaciones físicas.
Luego, al estudiar más a fondo la solución de las ecuaciones correspondientes se revela una estructura matemática más profunda y trascendental. En esos casos podemos afirmar que dicho fenómeno es como una especie de laboratorio que la naturaleza nos regala para formular las leyes físicas, o incluso para explorar nuevas áreas de las matemáticas. Con todas esas observaciones podemos formular teorías físicas completas, que podrían considerarse como una de las formas más sofisticadas del conocimiento humano. Un aspecto que muestra el poder de dicho conocimiento es la posibilidad de predecir fenómenos naturales completamente nuevos, a partir de analizar las soluciones matemáticas.

Sin duda este es el caso del fenómeno de colisiones o choques, algo que puede presentarse en muchos contextos, desde una pelota que se golpea con un bat o una raqueta, también cuando una bala o proyectil impactan otro objeto. Un meteorito que se acerca a la tierra es también un ejemplo de una colisión. Los jugadores de futbol americano que se encarreran para chocar e impedir el paso del oponente son también un choque.
Todas esas colisiones, que son parte del movimiento en general, se describen mediante la mecánica clásica, las leyes de Newton, que es la formulación más conocida, aunque también están las de Lagrange y Hamilton. En algunos casos los cuerpos que chocan mantienen su forma, y se dice que es un choque elástico, en cambio cuando los cuerpos se parten después de la colisión se les llama choques inelásticos.
En el mundo subatómico, donde aparecen los fenómenos cuánticos, el uso de las colisiones o choques juega también un papel muy importante. El estudio de choques entre átomos se remonta al tiempo de Ernest Rutherford, quien a principios del siglo XX logró identificar la distribución de la carga eléctrica del átomo. Una parte del mismo tenía que ser positiva, para equilibrar la carga negativa de los electrones, necesaria para así mantener la estabilidad eléctrica del átomo. El descubrimiento de la carga negativa ocurrió un poco antes, en 1897, y se debe a J.J. Thomson, el profesor de Rutherford, esa carga negativa es el electrón. Ahora sabemos que el electrón es una parte del átomo, y es de una naturaleza fundamental, pues no se puede dividir en componentes más básicos.
El experimento de Rutherford consistió en hacer chocar partículas alfa, que en realidad son los núcleos del átomo de Helio, sobre una placa de oro, muy delgada. El resultado que obtuvo Rutherford fue que las partículas alfa rebotaban en diferentes ángulos, incluso a 180 grados, mismo que podía interpretarse como resultado de colisiones entre las partículas alfa con otro objeto, de una masa mucho más grande que la del electrón, cuya carga eléctrica estaba concentrada en un radio muy pequeño. Dicho experimento dio lugar a la identificación del núcleo atómico, como la contraparte de carga positiva que equilibraba la carga negativa del electrón.
Por otra parte, cuando se intentó aplicar la física clásica para describir los fenómenos atómicos se encontró que eso no era posible. Por ejemplo, según la física clásica el electrón al estar girando en el átomo, debía emitir radiación electromagnética, misma que le haría perder energía y eventualmente caer en el núcleo atómico, así que no deberían existir los átomos según la física clásica.
La salida a este dilema llegó con la formulación de la Mecánica Cuántica. En la etapa temprana de su desarrollo participaron desde Max Planck, que propuso la idea de que la energía venía en cantidades discretas llamadas quantums, luego Niels Bohr aplicó la cuantización para el momento angular y lo aplicó para explicar en parte la estabilidad del átomo. El mismo Albert Einstein explicó el llamado efecto fotoeléctrico asumiendo que la luz consiste en partículas cuya energía está cuantizada. Los pasos siguientes se deben a otros gigantes de la física, incluyendo a Heisenberg, Pauli, Schrodinger, Dirac, Born, principalmente.
Erwin Schrödinger propuso una ecuación que lleva su nombre, misma que describe la evolución espacial y temporal de un ente matemático abstracto llamado “función de onda”, que contiene la información esencial de un sistema; a partir de la cual es posible calcular la energía de los estados del átomo de hidrógeno. La diferencia de energía entre dichos estados es justamente la energía de la radiación que puede emitir dicho átomo, lo cual fue ampliamente reconocido y un paso esencial para completar la teoría cuántica.
Otro paso importante se debe a W. Heisenberg, quien propuso que las cantidades dinámicas, como la posición y el momento, no son simples números sino objetos matemáticos que llamamos operadores, y que en su forma más simple se pueden representar por matrices. La formulación se completó gracias a Max Born, quien presentó una interpretación de la función de onda, como una probabilidad, algo que describía muy bien las observaciones atómicas, pero que implicaba abandonar la descripción determinista propia de la física clásica. Esta nueva visión del mundo sub-atómico causó mucha controversia, al grado que fue rechazada por muchos físicos, incluido Albert Einstein.
Regresando al tema del artículo, sobre las colisiones, resulta que cuando un electrón choca con un átomo, no podemos predecir con total certeza lo que ocurrirá. Resolviendo las ecuaciones que describen el sistema, podemos calcular la función de onda del electrón final, y con ello podemos calcular la probabilidad de que el electrón se disperse en un cierto ángulo, y con cierta energía.
Durante buena parte del siglo XX, se utilizó ese tipo de experimento de colisiones entre un haz de partículas que incidía sobre un blanco fijo, con ello se pudo descubrir la estructura del átomo y luego del mismo núcleo atómico. Así aprendimos que el átomo estaba formado de núcleo y electrones, mientras que el núcleo está formado de protones y neutrones. Más aún, durante los años 60 del siglo XX se estudió el choque entre electrones y los protones y neutrones del núcleo atómico, entonces se descubrió que los protones y neutrones están formados de algo más fundamental, llamados inicialmente partones, pero que concedía con los llamados quarks.

A mediados del siglo XX, luego de la conclusión de la segunda guerra mundial, los físicos de la generación de Feynman, Schwinger, Tomonaga, lograron construir un marco consistente para describir fenómenos cuánticos y relativistas, la grandiosa teoría de los Campos cuánticos (QFT, por sus siglas en Inglés). Con ella se pueden calcular procesos físicos que involucran las partículas elementales, tales como secciones transversales, tiempos de decaimiento, asimetrías, etcétera.
En el caso de una teoría física fundamental, como la Electro-dinámica Cuántica, que describe correctamente las interacciones electromagnéticas entre partículas cargadas, se puede describir mediante una formula complicada, que llamamos el Lagrangiano, cuya solución exacta no se conoce, por lo que recurrimos a métodos aproximados. Dichas aproximaciones pueden describirse como una serie potencias en una constante fundamental, que es la carga eléctrica.
Hay diversas maneras de trabajar dicha teoría, sin embargo se dice que la teoría llegó a las masas gracias al enfoque de Richard Feynman, quien inventó un lenguaje geométrico que contiene la información esencial de los procesos físicos. Dicho lenguaje se conoce como los diagramas de Feynman. Cada diagrama representa un término de la serie, y los mismos incluyen: vértices asociados con las interacciones, lineas internas que describen las partículas virtuales, y líneas externas asociadas con las partículas iniciales y finales de una colisión. Cada uno de esos elementos tiene asociado una fórmula matemática, tal que el proceso de juntarlos para obtener la probabilidad del choque, es como armar un juego de lego con cada uno de esos elementos. Así la amplitud de probabilidad para el proceso en el cual chocan un par electrón-positrón, para convertirse en un par de muon y anti-muon, le corresponde al primer orden el siguiente diagrama (Fig. 1):
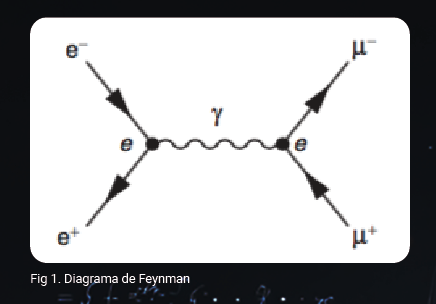
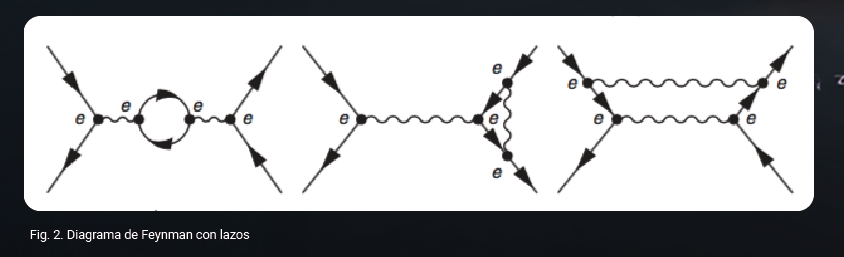
Dicho diagrama se le conoce como nivel árbol, ya que no contiene líneas cerradas o lazos, como si lo incluyen los diagramas del siguiente orden, por ejemplo:
Durante buena parte del siglo XX, y lo que llevamos del actual, los diagramas de Feynman nos permitieron calcular los procesos relevantes para los experimentos que se realizaron en aceleradores, y con ello se lograron muchos descubrimientos que permitieron comprender la física de las interacciones y partículas fundamentales de la naturaleza. Así se descubrieron los quarks pesados (charm, beuaty y top), también las partículas mediadoras de la interacción débil, W y Z, así como el gluon, el mediador de las interacciones fuertes.
Este éxito tuvo su clímax con el descubrimiento del bosón de Higgs en el acelerador LHC del CERN, anunciado el 4 de julio de 2013. El LHC hace chocar protones contra protones, alcanzando energías tan altas (13.5 TeV), que en realidad se logra hacer chocar a los quarks y gluones que forman el protón. Así, un mecanismo que contribuye a la producción del Higgs es la fusión de gluones que producen un estado virtual de quarks top, que a su vez se aniquilan para producir el Higgs; luego el Higgs puede decaer en un par de fotones o muones (Fig. 3).
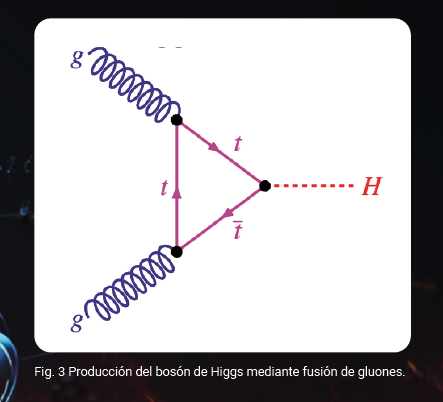
El estudio de dichas colisiones se hace mediante la aplicación de la cromo dinámica cuántica, la teoría de las interacciones fuertes. Esta teoría es una teoría cuántica de campos, aunada con una simetría interna que asocia un campo de fuerza con los generadores del grupo de simetría, esos son objetos asociado con la estructura matemática de la teoría de grupos.
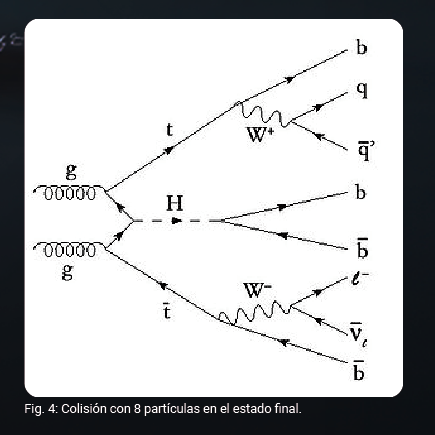
El resultado de esta síntesis, se conoce como teoría cuántica de campos normados. Siendo cuántica quiere decir que solo podemos calcular la probabilidad de que ocurra un proceso. Así cuando chocan un quark y un antiquark, se pueden producir muchos estados diferentes. El proceso dominante involucra el mínimo posible de partículas en el estado final, que puede ser un par de quarks pesados, o muones. También es posible tener una reacción 2-> 3, con dos partículas iniciales que producen varias partículas finales, en la Fig. 4 se muestra la reacción para producir dos quarks top y un Higgs, y cuando incluyen los decaimientos quedan 8 partículas en el estado final. La complicación matemática hace muy difícil calcular procesos con más de 4-5 partículas en el estado final con los métodos de Feynman.
Sin embargo, cuando algo empieza a complicarse tanto, los físicos se inspiran para buscar otra manera más fácil de hacer los cálculos. En años recientes de ha avanzado para entender más a fondo el formalismo de la QFT; estos avances han permitido encontrar una nueva manera de hacer cálculos de colisiones cuánticas que involucran quarks y gluones, con la cual es posible calcular reacciones que no se pueden realizar con los métodos tradicionales de los diagramas de Feynman.
Así, al final del siglo pasado algunos físicos encontraron que si se especificaban los números cuánticos de las partículas participantes en la colisión (método de helicidad) era posible realizar cálculos complicados. De hecho Parke y Taylor encontraron una fórmula, que lleva su nombre, para calcular una reacción con un número arbitrario de gluones, con una configuración específica de helicidades (MHV). Esto lo hicieron calculando a pico y pala, pero la fórmula final era tan bella, algo que parecía imposible de simplificar con los métodos tradicionales, que decidieron lanzaron un reto a la comunidad de teóricos para demostrar dicha fórmula. Eso se logró, en parte gracias al trabajo de Bern, Dixon y Kosower, y los avances se fueron consolidando como un método alternativo para hacer cálculos en QFT. Llegaron luego otros refuerzos de lujo, como Witten y Arkani-Hamed, junto con otros jóvenes como Britto, Cachazo, Feng et al, que lograron consolidar el tema bajo el nombre genérico de Amplitudes, tal que cada año se realiza una conferencia que se llama así, Amplitudes.
Este método hace uso de las simetrías que obedecen las ecuaciones de campo. Las colisiones dependen de la energía y el momento asociado con cada partícula que participa en la colisión. De hecho el método parte de hacer una especie de cambio de variables para pasar el 4-momento a variables espinoriales de 2 componentes.
Actualmente, bajo el paraguas llamado Amplitudes, se incluyen desde métodos para realizar cálculos prácticos para el LHC, hasta una reformulación de la QFT basada solamente en elementos medibles (llamada Constructive QFT), pasando por el uso de las matemáticas más avanzadas y complejas para geometrizar el cálculo de amplitudes (conel llamado Amplutuhedron). Un bono de estos métodos ha sido el sorprendente descubrimiento de que los cálculos en QCD permiten derivar las fórmulas para el cálculo de procesos que involucran a los gravitones, que resultan ser el cuadrado de las amplitudes que se obtienen con la Cromodinámica Cuántica (QCD, la teoría de los quarks y gluones). De modo que se puede decir que Quantum Gravity es Yang-Mills al cuadrado.
Muchas joyas nos ha dejado la exploración de las colisiones cuánticas y sin lugar a dudas todavía deben quedar muchas estructuras matemáticas ricas esperando ser descubiertas, para quien se atreva a caminar por el sendero de Swann.
Lorenzo Díaz Cruz
Es doctor en Física por la Universidad de Michigan. Obtuvo el Premio Estatal Puebla de Ciencia y Tecnología en 2009. Fue merecedor de la Medalla de la DPyC–SMF (División de Partículas y Campos, Sociedad Mexicana de Física) en 2003 por su trayectoria en física de altas energías. Pertenece al SNI Nivel III. Realizó estudios en temas de educación en el Seminario CIDE–Yale de Alto Nivel en 2016. Es autor del libro El muchacho que soñó con el bosón de Higgs.



